Apprenez À Rencontrer L’équation Réduite De La Droite Qui Passe Par Les Points. Suivez Nos Étapes Claires Pour Maîtriser Cette Compétence Essentielle En Mathématiques.
**graphiques : Visualiser L’équation Réduite**
- Comprendre L’équation Réduite Et Ses Enjeux
- Importance Des Graphiques Dans L’interprétation Mathématique
- Outils Numériques Pour Visualiser L’équation Réduite
- Étapes Pour Créer Un Graphique De Qualité
- Applications Pratiques Des Graphiques Dans La Vie Quotidienne
- Erreurs Courantes À Éviter Lors De La Visualisation
Comprendre L’équation Réduite Et Ses Enjeux
L’équation réduite, souvent considérée comme la pierre angulaire de l’analyse mathématique, offre une vision simplifiée des relations linéaires entre des variables. En la maîtrisant, on se rapproche d’une compréhension plus profonde des systèmes que l’on cherche à modéliser. Imaginez-vous dans un monde où chaque donnée est un composant essentiel, comme les médicaments dans une pharmacie. Pour prescrire un traitement efficace, il faut savoir analyser non seulement les symptômes, mais aussi les interactions possibles entre les médicaments, tout comme une équation qui relie divers éléments. Cela illustre l’importance de bien appréhender cette forme d’équation, surtout dans un domaine où les mesures et les résultats peuvent s’avérer critiques.
Les enjeux entourant l’équation réduite sont multiples. Ils vont des calculs les plus élémentaires aux défis plus complexes rencontrés dans des domaines variés, comme l’économie, la biologie, ou même la médecine. En effet, une mauvaise interprétation peut non seulement entraîner des erreurs dans les résultats mais aussi des conséquences concrètes, visibles dans des situations telles que la gestion de médicaments. Par exemple, un script mal rédigé peut conduire à des erreurs de dosage chez un patient, illustrant ainsi l’importance de la clarté dans la formulation. Dans ce contexte, table de l’équation réduite peut servir de guide, semblable à un élixir de connaissance, permettant de naviguer facilement dans les complexités des mathématiques.
| Équation | Application |
|---|---|
| y = mx + b | Modélisation des ventes |
| A = l × h | Calcul de l’aire |
| v = d / t | Calcul de la vitesse |
Importance Des Graphiques Dans L’interprétation Mathématique
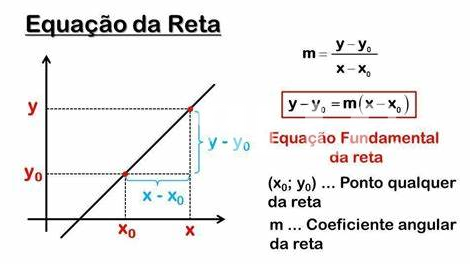
Les graphiques jouent un rôle capital dans l’interprétation des concepts mathématiques. En représentant visuellement des informations, ils permettent aux apprenants de saisir des relations complexes que les chiffres seuls peinent à transmettre. Par exemple, lorsque l’on cherche à encontre la équation réduite da reta qui passa pelos pontos, un graphique peut illustrer de manière immédiate comment ces points se connectent, facilitant ainsi la compréhension des notions de pente et d’ordonnée à l’origine. La synthèse visuelle d’une équation ouvre des perspectives qui peuvent parfois sembler obscures dans un contexte purement numérique.
De plus, les graphiques rendent les données plus accessibles et mémorables. En ajoutant des couleurs, des formes et d’autres éléments visuels, ils permettent de transformer des informations abstraites en vérités concrètes. Cela est particulièrement bénéfique dans le domaine de la santé, où une représentation graphique des prescriptions médicinales aide à comparer différentes options ou à visualiser l’effet d’un traitement dans le temps. Comprendre ces éléments graphiques, c’est également comprendre les histoires qu’ils racontent, une compétence essentielle pour quiconque souhaite approfondir ses connaissances en mathématiques.
Enfin, les graphiques servent d’outil d’analyse dans la prise de décision. Ils sont essentiels pour repérer des tendances et des anomalies qui pourraient passer inaperçues dans des tableaux de données bruts. Par exemple, les analyses des données de ventes ou des performances dans le secteur pharmaceutique peuvent être grandement améliorées par l’usage des graphiques, permettant ainsi une réaction plus rapide – stat – aux besoins du marché. En somme, ces outils visuels ne sont pas qu’une simple décoration, mais des éléments indispensables pour une interprétation claire et efficace des équations en mathématiques.

Outils Numériques Pour Visualiser L’équation Réduite
Dans le monde numérique d’aujourd’hui, il existe une multitude d’outils qui nous permettent de représenter graphiquement l’équation d’une droite, facilitant ainsi la compréhension de concepts mathématiques fondamentaux. Les logiciels comme GeoGebra ou Desmos sont particulièrement appréciés pour leur interface intuitive. En quelques clics, il est possible d’entrer une équation et de visualiser instantanément le graphique correspondant. Par ailleurs, ces plateformes offrent la possibilité d’interagir en temps réel avec les graphiques, ce qui permet d’explorer comment la modification des coefficients affecte la pente et l’ordonnée à l’origine. En outre, avec la phrase célèbre “encontre a equação reduzida da reta que passa pelos pontos”, ces outils aident les utilisateurs à déterminer précisément les valeurs qui définissent une droite passant par des points donnés.
De plus, certains outils avancés, comme MATLAB ou Python avec la bibliothèque Matplotlib, permettent une personnalisation poussée des visualisations. Ces programmes sont idéaux pour les utilisateurs qui souhaitent aller au-delà des simples tracés en intégrant des analyses statistiques. Par exemple, ils peuvent générer des graphiques dynamiques qui illustrent comment une droite s’adapte à différents ensembles de données. Bien qu’ils demandent une certaine courbe d’apprentissage, leur potentiel est immense, notamment dans les études de cas complexes. En utilisant ces outils numériques, non seulement les étudiants peuvent mieux comprendre le concept de l’équation réduite, mais ils peuvent aussi développer des compétences techniques qui leur seront indispensables dans leur parcours académique et professionnel.
Étapes Pour Créer Un Graphique De Qualité
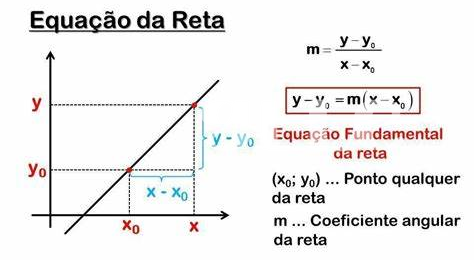
Pour créer un graphique de qualité, il est essentiel de commencer par bien comprendre l’équation réduite de la droite. Cette équation, qui représente une relation linéaire entre deux variables, vous permet d’établir des points clés sur votre graphique. Pour cela, il faut d’abord identifier les coordonnées des points par lesquels la droite passe. En rencontrant l’équation réduite de la droite qui passe par ces points, vous pouvez ainsi déterminer la pente et l’ordonnée à l’origine.
Ensuite, il est important de choisir les outils adéquats pour dessiner le graphique. Que ce soit avec un logiciel comme GeoGebra ou même à la main sur du papier millimétré, la précision est la clé. Une fois votre espace de travail préparé, commencez par tracer les axes correctement, en utilisant des échelles appropriées. N’oubliez pas que des graphiques mal étiquetés peuvent entraîner des confusions, tout comme les stupéfiantes prescriptions qui peuvent être mal attribuées.
Le choix des couleurs et des styles de lignes doit également être réfléchi. Utilisez des couleurs contrastantes pour rendre le graphique plus lisible et engageant. De plus, l’inclusion de légendes et de titres clairs peut aider à mieux expliquer votre graphique. Parfois, un simple “drive-thru” pour faire le tri entre les différentes données peut rendre votre travail beaucoup plus net et organisé.
Enfin, une fois le graphique terminé, prenez le temps de l’évaluer. Examinez si toutes les informations sont présentes et si le message que vous souhaitez transmettre est clair. N’hésitez pas à demander des retours à vos pairs; leur perspective peut vous aider à éviter des erreurs courantes qui pourraient, autrement, rendre votre graphique moins efficace. En faisant ces vérifications, vous maximisez la valeur informative de votre visuel, tout en vous assurant que le public puisse en tirer le meilleur parti.

Applications Pratiques Des Graphiques Dans La Vie Quotidienne
Dans notre vie quotidienne, les graphiques jouent un rôle fondamental qui transcende les simples numéros et données. Par exemple, lorsqu’il s’agit de planifier un budget personnel, un graphique peut facilemnt visualiser l’évolution de nos dépenses par rapport à nos revenus. Cela permet non seulement de prendre des décisions éclairées, mais également d’identifier rapidement les domaines où des ajustements sont nécessaires. En outre, pour les étudiants en mathématiques, la capacité à rencontrer l’équation réduite de la droite qui passe par différents points est un outil crucial. Cela leur permet non seulement de résoudre des problèmes d’équations, mais également de comprendre des concepts plus profonds liés à la géométrie et à l’analytique.
Un autre exemple frappant d’application de graphiques se trouve dans le domaine de la santé. En utilisant des graphiques pour suivre des indicateurs de santé, comme la pression artérielle ou le taux de cholestérol, les patients peuvent discuter plus efficacement de leur santé avec leur médecin. Cela favorise une meilleure communication et aide à ajuster les prescriptions, c’est pourquoi il est important de renforcer les compétences analytiques en matière de données. De plus, dans un environnement comme une pharmacie lors de ce qu’on appelle “le Pharmageddon”, les graphiques peuvent aider les pharmaciens à gérer leur charge de travail, en visualisant rapidement les tendances dans la prescription de médicaments. Ces outils ne sont pas seulement théoriques; ils sont essentiels pour la prise de décisions pragmatiques et efficaces dans de nombreuses situations de la vie quotidienne.
| Application | Utilité |
|---|---|
| Budget Personnel | Identifier les dépenses et ajuster les budgets |
| Santé | Suivi des indicateurs de santé pour discussions avec le médecin |
| Pharmacie | Gestion des prescriptions durant des périodes chargées |
Erreurs Courantes À Éviter Lors De La Visualisation
Lors de la visualisation de l’équation réduite, certaines erreurs peuvent sérieusement altérer la clarté et l’interprétation des résultats. Tout d’abord, il est courant de négliger l’étiquetage des axes. L’absence d’étiquettes claires peut rendre les graphiques difficiles à comprendre, même pour ceux qui ont une certaine expérience en mathématiques. Une simple référence comme “x” et “y” peut sembler suffisante au début, mais cela ne fournit pas le contexte nécessaire pour interpréter les données. Un graphique sans légende ou avec des couleurs mal choisies peut se transformer en un véritable “pill mill” de confusion.
Ensuite, l’échelle des axes est un autre piège fréquent. Une échelle inadéquate peut déformer la réalité des données. Par exemple, zoomer sur une petite partie d’un graphique peut donner une fausse impression de tendance. Il est crucial de veiller à ce que l’échelle soit proportionnelle et ajuste le contenu de manière appropriée. En omettant ce détail, on peut se retrouver avec un graphique qui donne l’illusion d’une tendance significative alors que ce n’est pas le cas, un peu comme des “happy pills” qui masquent des problèmes sous-jacents.
Une autre erreur à éviter est le surchargement d’information. Trop d’éléments visuels peuvent rendre le graphique chaotique. Cela est parfois comparable à un “cocktail” de données où chaque ingrédient semble important, mais où la combinaison crée finalement une toxique confusion. La simplicité est parfois la clé, permettant de transmettre l’essentiel sans embrouiller l’esprit du lecteur.
Enfin, ignorer le public cible lors de la création d’un graphique peut être désastreux. Chaque audience a ses propres niveaux de connaissance et ses attentes. Prendre le temps de considérer qui regardera le graphique peut aider à le structurer de manière à ce qu’il soit à la fois engageant et informatif. Tout comme un “med check” où l’on s’assure que les patients comprennent bien leurs traitements, il est crucial de s’assurer que le message que l’on veut transmettre à travers le graphique soit non seulement clair, mais aussi accessible.
